Cyclesボリューム アラモード
空みたいな青いスイーツは大体着色料ということを全国のちびっこが知ってしまった2017年も終わりが近づいてまいりました。
これはBlender Advent Calendar 2017に飛び込みでつっこんだ記事です。
少し前にTwitterでホットボンドの芯を使ってレイリー散乱の実験をするというツイートを見かけました。
なかなかそれっぽくて面白かったので、Blenderでこれをやってみましょう。
Internal
BlenderのInternalレンダラーでもボリュームをレンダリングすることができます。 しかしマテリアルノードを利用できないようです。 無理やりやるならグラデーションのテクスチャを使ってそれっぽく見せるくらいはできるでしょう。 ただそれでは光源の位置や数に合わせてテクスチャをいい感じに調整しないといけません。
それはとても面倒です。
Cycles
というわけでCyclesでやりましょう。
まずはシーンの準備です。
ボリュームは結構サイズが見た目に効いてくるので、なるべく実物と同じ寸法でセッティングすることにします。 検索してみるとホットボンドの芯は直径7mmで長さが10cmの円柱が一般的なようです。
それから光源はとりあえず点光源を使います。スマートフォンのフラッシュに使われるLEDくらいのものを想定してサイズを2mmとしておきました。 このランプのところにあるサイズの設定は忘れがちで、特に小さなものを作ると光源が物体にめり込んでおかしなレンダリング結果になったりするのはよくあることなので注意です。 私だけかもしれませんが。

こんなものでしょうか。背景に板を置いたら照り返しがすごかったので光源は黒い筒に入れました。
次に本命のマテリアルです。
Cyclesのボリュームマテリアルはお手軽で、マテリアルノードのボリューム(Volume)に"ボリュームの散乱(Volume Scatter)"や"ボリュームの吸収(Volume Absorption)"を繋ぐだけです。 とりあえずレイリー散乱の実験だったので、ボリュームの散乱を繋げてみるとこんな感じになりました。
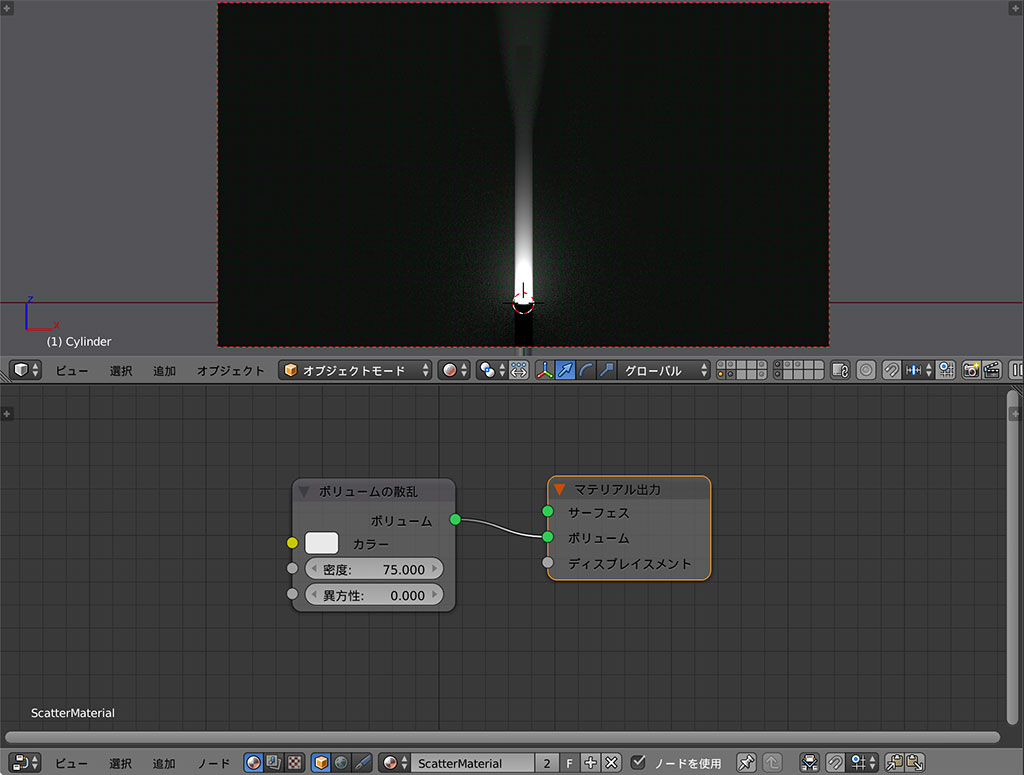
レイリー散乱では光の波長が散乱の強さに関わってくるそうですが、残念ながらCyclesは波長を考慮するレンダラーではないのでそのような設定項目はありません。 ではどうしようかとなりますが、少し使い込んだ方なら似たようなものをキラッとひらめくのではないでしょうか。
屈折で起こる光の分散(Dispersion)です。
光の分散を再現したガラスのマテリアルはちょっと検索すると簡単に例が見つかります。 やたら凝ったものもありますが、基本的な考え方は一旦RGBに分離してそれぞれに違う屈折率を設定し、再び合成するというものです。 Cyclesはサーフェスもボリュームも同じ理論の元でレンダリングされるので、同じ考え方がボリュームでも使えるのではないかというわけです。
それではボリュームの散乱にRGB単色のカラーを設定して、それぞれの値を適当にずらして合成してみると…

割とそれっぽいです。
できあがり!
CGは科学です
フィーリングでそれっぽいでもいいのですが、物理ベースが流行りの昨今、それなりに根拠のある数値を設定したくなります。
そこでまずはレイリー散乱を調べてみるとこんな数式が出てきました。
文字がたくさんありますがほとんどは物質の性質によって決まる値です。 あとで見やすいようにちょっと変形しておきます。
RGBの割合
それではとりあえずRGBの各成分の割合を決めたいと思います。
そのためには各色の波長が必要です。これはCIE(国際照明委員会)によって決められたものがあります。
単位はナノメートルです。
次にレイリー散乱の数式から波長によって変化する部分だけを抜き出します。
レイリー散乱の数式を見ると、波長 の影響があるのは
の部分だけです。
そこでRGBそれぞれの値を計算してみるとこのようになります。
Bの波長から求めた値が一番大きいのでこれを基準にすることにします。 RとGの波長から求めた値をBの波長から求めた値で割って、各成分との比率を求めます。
この値をボリュームの散乱のカラーに設定すれば良いでしょう。
位相関数
ところでボリュームの散乱に"異方性(Anisotropy)"というパラメーターがあるのが気になります。
Cyclesのサーフェスのシェーダーは"****BSDF"という名前がついています。BSDFとはおなじみ、双方向散乱分布関数です。 では"ボリュームの散乱"は何かというと、位相関数(Phase Function)と呼ばれるものに相当します。 CyclesではHenyey-Greensteinの位相関数というものを使っているようです。
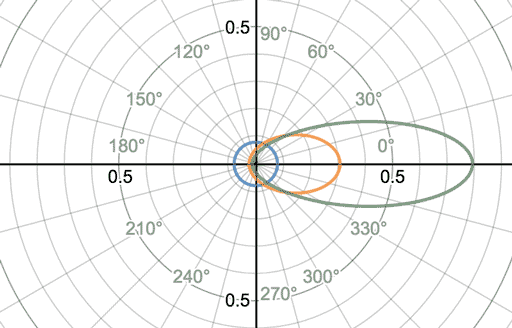
数式はこちら。グラフで遊べます。 ここではgがノードの異方性に当たります。
異方性の値が0なら等方散乱、+に設定すると前方散乱、-に設定すると後方散乱を表現することができます。 前方、後方とは何かという感じですが簡単に説明すると、まず散乱というのは光が全ての方向に散ってしまうことです。 このグラフは左側から来た光が原点(0,0)のところで散乱した時に、それぞれの方向に散らばる量を示しています。 実際には三次元なのでこれを光の進行方向の軸でぐるっと回してできた回転体の形になります。 そしてこれがどんな風にレンダリング中に使われるかというとこんな感じです。
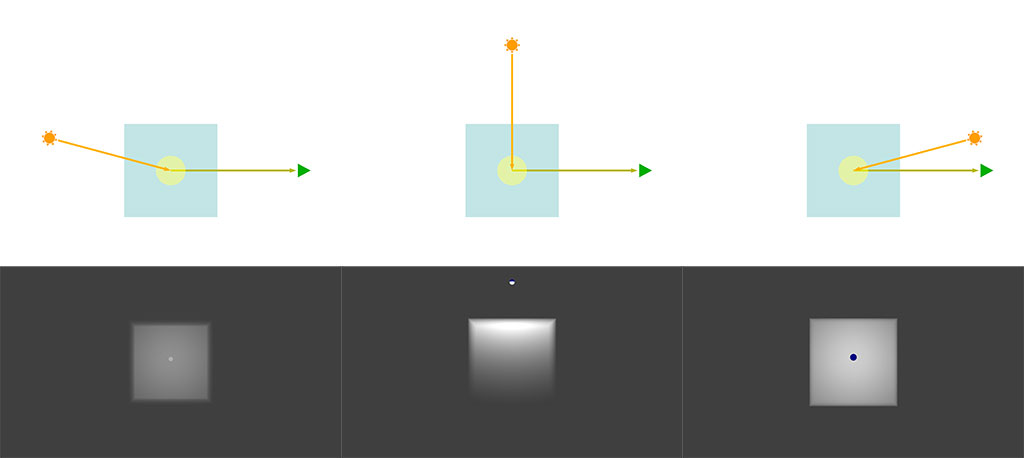
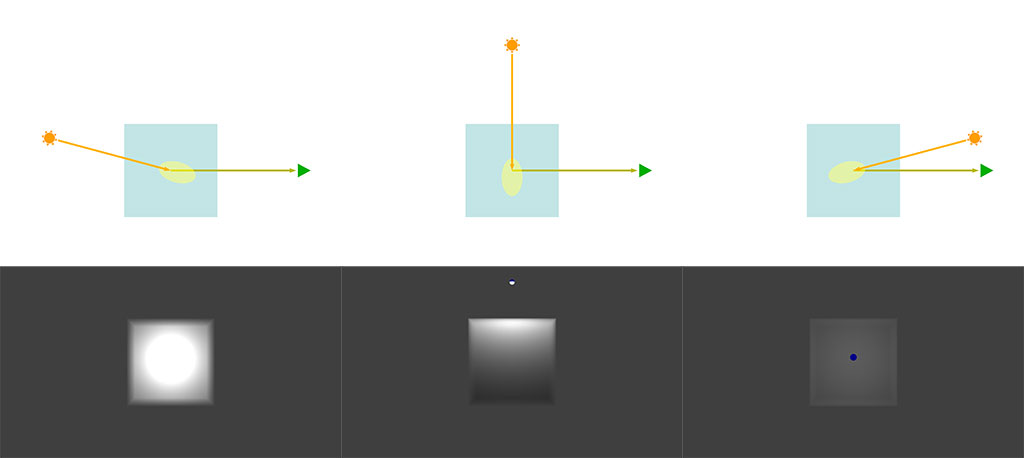
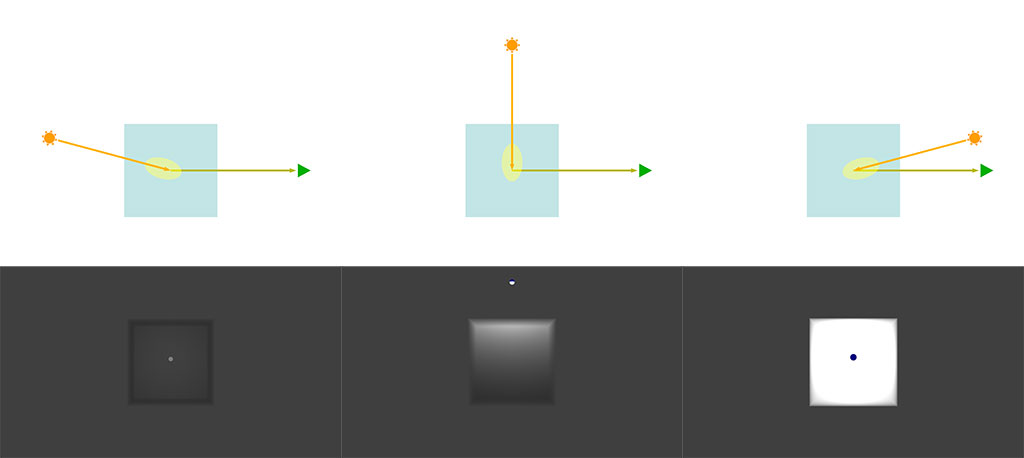
前方散乱、後方散乱という意味がなんとなくわかるでしょうか。 右側の緑の三角がカメラで、薄い青の部分がボリュームと考えてください。真ん中の黄色いものがその位置で求めた位相関数の値のグラフになります。 これを基にして視点の方に向かう光の量を求めることができます。 実際のレンダリングではボリューム内で視線の先にそっていくつもの点をとり、ボリュームに入ってから抜けるまでの値を積分して求めます。
さて、若干話が逸れ気味でしたが、レイリー散乱がどのような散乱になるかを調べます。
数式から視線と光源との角度に依存する部分を抜き出してみると になります。
このグラフを書いてみるとこんな感じです。
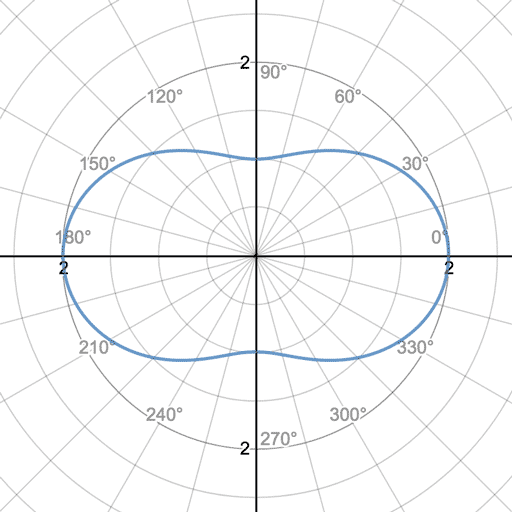
色々な定数を無視しているので、大きさは実際とは異なります。 とはいえそのままでは似たような感じにはならなさそうです。 このような時は複数のボリュームの散乱をミックスして近似することができます。 前方散乱と後方散乱を組み合わせれば似たような感じになりそうなのでやってみましょう。
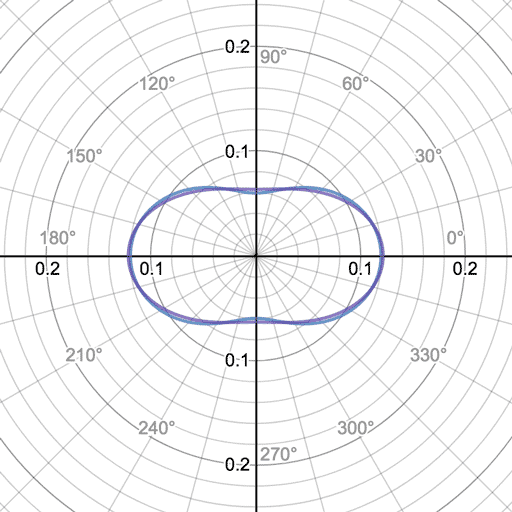
紫がミックスしたものですがこんなものでしょうか。異方性0.3と-0.3をミックスするとこんな感じになりました。
なお最初に科学ですと言いましたがなんとここは目分量ですw

異方性0と比較して見ると左右の前方と後方の散乱が少し多くなって、視線と垂直になる真ん中が心持ち少なくなっているように見えます。
レッツラまぜまぜ
RGBの割合と、散乱のシェーダーを合わせてみるとこんな感じになります。
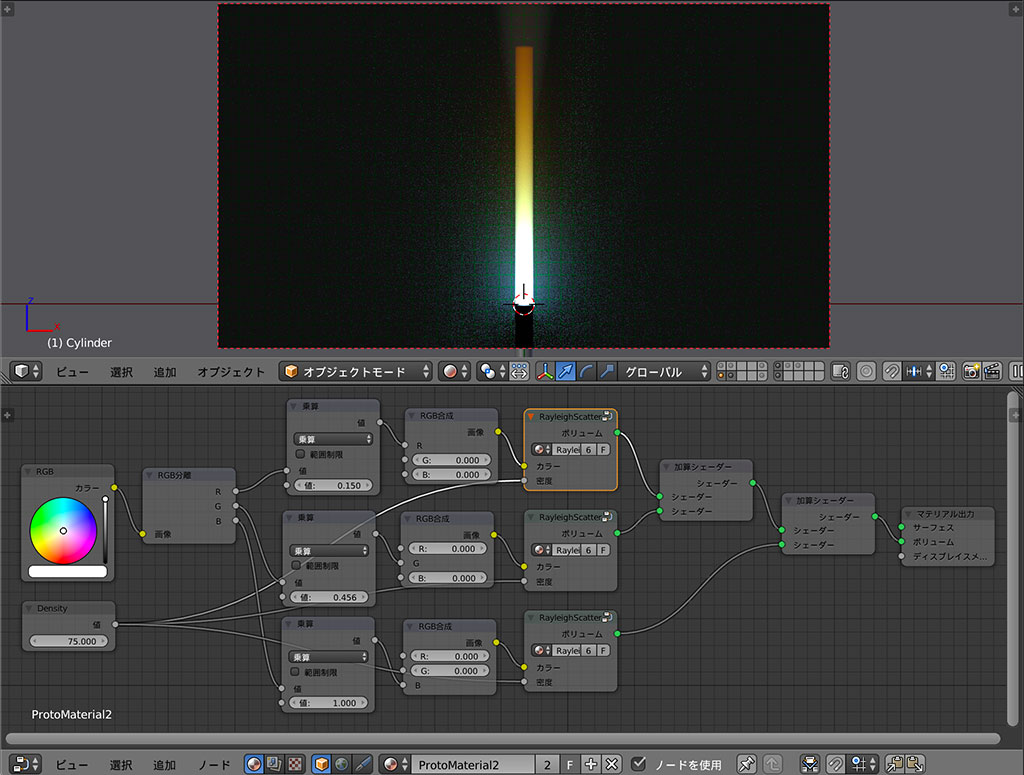

パルフェ!
ボナペティ!
あとはサーフェスのシェーダーを適当に組み合わせて棒に見えるようにしましょう。 フレネルで透過(Transparent)BSDFと光沢(Glossy)BSDFをミックスしました。
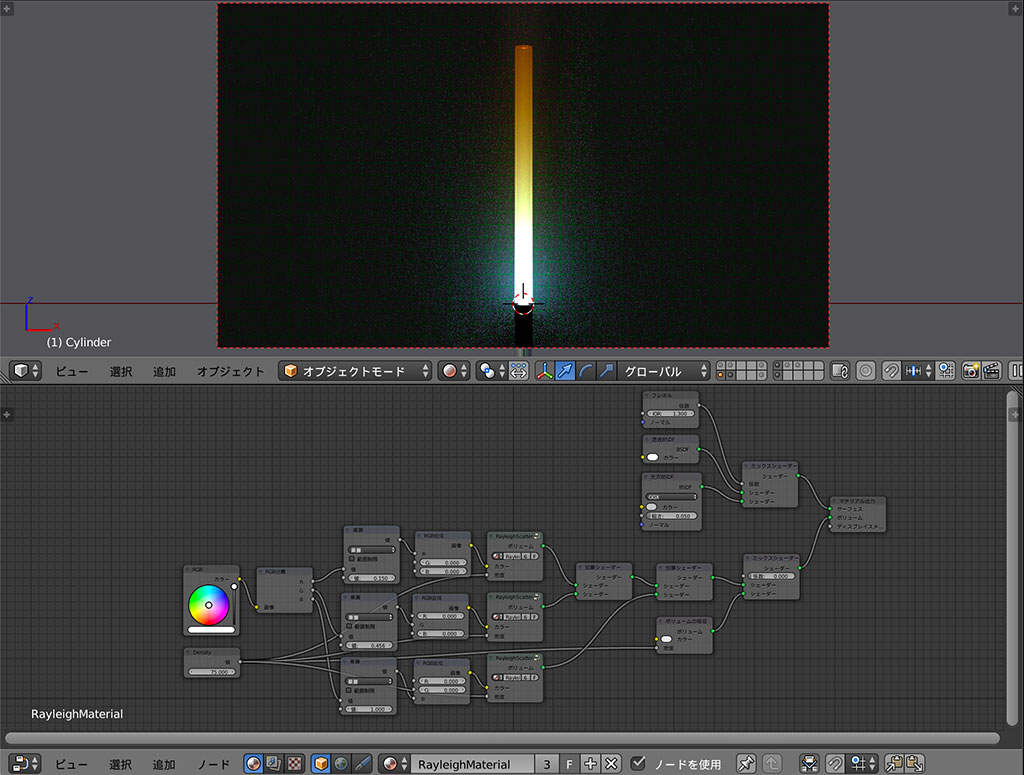
ボリュームの散乱の密度を1から100まで変化させてみるとこうなります。

思ったよりもそれっぽくなりました。素敵です。
最後に、ボリュームはノイズが多くなりやすいですが見た目はぼんやりしたものなので、デノイズがとても有効です。 活用しましょう。
明日はmelrosecoolさんです。 まだまだ空きもありますよ!